Machine Learning Notes
-
随机模拟 蒙特卡洛算法(Monte Carlo)
-
直接采样、接受-拒绝采样、重要性采样
-
马尔可夫链 (Markov Chain)
定义见https://pages.uoregon.edu/dlevin/MARKOV/ 缓存
-
irreducibility and aperiodicity
A chain P is called irreducible if for any two states $x,y$ there exists an integer t (possibly depending on x and y) such that
\[P^t(x,y) > 0\]This means that it is possible to get from any state to any other state using only transitions of positive probability.
否则的话,所有状态就像有一个高度,状态只能从上到下转移或平行转移,不能从下到上转移。
Let \(\mathcal{T}(x) = \{ t \in \mathbb{Z}^+ : P^t(x,x) > 0\}\) The period of state $x$ is defined to be the GCD of $ \mathcal{T}(x) $.
The chain will be called aperiodic if all states have period 1. If a chain is not aperiodic, we call it periodic.
-
MCMC M-H and Gibbs
https://cosx.org/2013/01/lda-math-mcmc-and-gibbs-sampling 缓存
-
-
-
EM Algorithm
-
Notation
bold font $ \textbf{x} $ are vector, superscript $ \textbf{x}^{(i)} $ are i-th sample.
-
Formula Deduction
\[\begin{align} \ell(θ) &= \sum_{i=1}^{m}{\log{p(\mathbf{x}^{(i)}; θ)}} \;\;\;\; & \text{log likelihood} \\ &= \sum_{i=1}^{m}{\log{\sum_{\textbf{z}^{(i)}}{p(\mathbf{x}^{(i)}, \textbf{z}^{(i)}; θ)}}} & \text{find latent var } \textbf{z}^{(i)} \text{behind } \mathbf{x} \\ &= \sum_{i=1}^{m}{\log{\sum_{\textbf{z}^{(i)}}{Q_{i}(\textbf{z}^{(i)})\frac{p(\mathbf{x}^{(i)}, \textbf{z}^{(i)}; θ)}{Q_{i}(\textbf{z}^{(i)})}}}} & \text{arbitrarily insert a distribution of }z^{(i)} \\ &= \sum_{i=1}^{m}{\log{\underset{\textbf{z}^{(i)}\sim Q_{i}}{E}\left[ \frac{p(\mathbf{x}^{(i)}, \textbf{z}^{(i)}; θ)}{Q_{i}(\textbf{z}^{(i)})} \right]}} & \text{treat }\frac{p(\mathbf{x}^{(i)}, z^{(i)}; θ)}{Q_{i}(z^{(i)})}\text{ as a random variable } \textbf{Z}_i \\ &≥ \sum_{i=1}^{m}{\underset{\textbf{z}^{(i)}\sim Q_{i}}{E}\left[\log \frac{p(\mathbf{x}^{(i)}, \textbf{z}^{(i)}; θ)}{Q_{i}(\textbf{z}^{(i)})} \right]} & \log(E[\mathbf{Z}]) ≥ E[\log(\mathbf{Z})],\text{equal holds iff } p(\mathbf{Z}=E[\mathbf{Z}])=1 \\ &= \sum_{i=1}^{m}{\sum_{\textbf{z}^{(i)}}{Q_{i}(\textbf{z}^{(i)}) \log \frac{p(\mathbf{x}^{(i)}, \textbf{z}^{(i)}; θ)}{Q_{i}(\textbf{z}^{(i)})}}} & \text{ by definition of expectation.} \end{align}\]Equal sign is achieved only when $ \textbf{Z} $ is almost a constant
\[\left\{ \begin{array}{l} Q_{i}{(\textbf{z}^{i})} \propto p(\mathbf{x}^{(i)}, \textbf{z}^{(i)}; θ) \\ \sum_{\textbf{z}^{(i)}}{Q_{i}{(\textbf{z}^{i})}} = 1 \end{array} \right.\]Hence:
\[Q_{i}(\textbf{z}^{(i)} = \textbf{u}) = p(\textbf{z}^{(i)} = \textbf{u} | \mathbf{x}^{(i)}; θ)\]Visualization (Image Source Cached (disable js to prevent force jump))
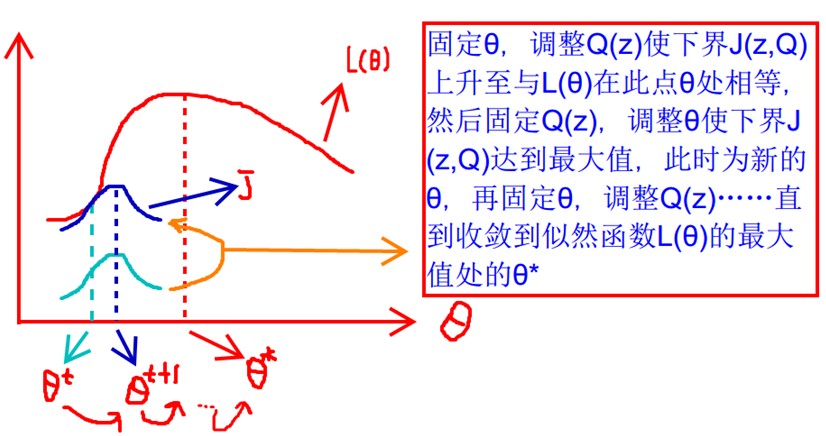
-
Algorithm
-
E-step: Set $ θ $ fixed. Find $ Q $ to maximize $ \mathbb{E}[\log(\textbf{Z})] $ to achive
\[\ell(\theta) = \sum_{i=1}^{m}{\log (\mathbb{E}(\textbf{Z}_i))} = \sum_{i=1}^{m}{\mathbb{E}[\log(\textbf{Z}_i)]}\] \[Q_{i}(\textbf{z}^{(i)} = \textbf{u}) := p(\mathbf{z}^{(i)} = \textbf{u} | \mathbf{x}^{(i)}; θ)\] -
M-step: Set $ Q_i $ fixed. Find $ θ $ to maximize $ \mathbb{E}[\log(\textbf{Z})] $
\[θ := arg \max_{θ} \sum_{i=1}^{m}{\sum_{\mathbf{z}^{(i)}}{Q_{i}(\mathbf{z}^{(i)}) \log \frac{p(\mathbf{x}^{(i)}, \mathbf{z}^{(i)}; θ)}{Q_{i}(\mathbf{z}^{(i)})}}}\]
-
-
Monotony
\[\begin{align} \ell(\theta^{t+1}) &= arg \max_{θ} \sum_{i=1}^{m}{\sum_{\mathbf{z}^{(i)}}{Q_{i}(\mathbf{z}^{(i)}) \log \frac{p(\mathbf{x}^{(i)}, \mathbf{z}^{(i)}; θ)}{Q_{i}(\mathbf{z}^{(i)})}}} & \\ &\geq \sum_{i=1}^{m}{\sum_{\mathbf{z}^{(i)}}{Q_{i}(\mathbf{z}^{(i)}) \log \frac{p(\mathbf{x}^{(i)}, \mathbf{z}^{(i)}; θ^t)}{Q_{i}(\mathbf{z}^{(i)})}}} & \\ &=\ell(\theta^t) &\\ \end{align}\] -
Why EM:
It is hard to directly optimize \(\sum_{i=1}^{m}{\log{p(\mathbf{x}^{(i)}; θ)}}\), while easier to deal with \(\sum_{i=1}^{m}{\log{\sum_{z^{(i)}}{p(\mathbf{x}^{(i)}, z^{(i)}; θ)}}}\)
-
Example: use EM to find GMM parameters:
\[θ := arg \max_{θ} \sum_{i=1}^{m}{\sum_{z^{(i)}}{Q_{i}(z^{(i)}) \log \frac{p(\mathbf{x}^{(i)}, z^{(i)}; θ)}{Q_{i}(z^{(i)})}}}\]where \(θ\) is a set of parameter \((\mathbf{ϕ,μ,Σ})\)
\[\begin{align} \text{Let } w_{j}^{i} = Q_i (z^{(i)}=j) &= p(z^{(i)}=j|\mathbf{x}^{(i)};ϕ,μ,Σ) \\ &= \frac{p(z^{(i)}=j,\mathbf{x}^{(i)};ϕ,μ,Σ)}{\underset{z^{(i)}}{\sum{}}{p(z^(i)=j,\mathbf{x}^{(i)};ϕ,μ,Σ)}} \end{align}\] \[\begin{align} J(Q,θ) &= \sum_{i=1}^{m}{\sum_{z^{(i)}}{Q_i (z^{(i)}) \log \frac{p(\mathbf{x}^{(i)},z^{(i)}; \mathbf{ϕ},\mathbf{μ},\mathbf{Σ})}{Q_i (z^{(i)})}}} \\ &= \sum_{i=1}^{m}{\sum_{j}{Q_i (z^{(i)}=j) \log \frac{p(\mathbf{x}^{(i)}|z^{(i)}=j;\mathbf{μ},\mathbf{Σ})p(z^{(i)} = j;ϕ)}{Q_i (z^{(i)}=j)}}} \\ &= \sum_{i=1}^{m}{\sum_{j}{w^{(i)}_j \log \frac{(2π)^{-\frac{n}{2}} |Σ_j|^{-\frac{1}{2}}exp{\left(-\frac{1}{2} (x^{(i)}-μ_j)^{T} Σ_j^{-1}(x^{(i)}-μ_j) \right)}ϕ_j}{w^{(i)}_j}}} \end{align}\]-
\(\partial \mathbf{μ_l}\).
\[\begin{align} \frac{∂J}{∂μ_l} \sim \frac{∂}{∂μ_l} \sum_{i=1}^{m}{w^{(i)}_{l}\left(-\frac{1}{2} (x^{(i)}-μ_l)^{T} Σ_l^{-1}(x^{(i)}-μ_l) \right)} \\ \sim \sum_{i=1}^{m}{w^{(i)}_{l} (x^{(i)}-μ_l)^{T} Σ_l^{-1}(-\mathbf{I})} \\ \sim \sum_{i=1}^{m}{w^{(i)}_{l} (μ_l-x^{(i)})^{T} Σ_l^{-1}} \\ \end{align}\]set to \(0\), we have
\[μ_l = \frac{\underset{i}{\sum{}}{w^{(i)}_{l}\mathbf{x}^{i}}}{\underset{i}{\sum{}}{w^{(i)}_{l}}}\] -
\(\partial ϕ_j\).
\[\begin{align} \frac{∂J}{∂ϕ_l} &= \frac{∂}{∂ϕ_l} \sum_{i=1}^{m}{w^{(i)}_{l} log ϕ_l} \end{align}\]also \(\sum_{j}{ϕ_j}=1\)
Use Lagrange multiplier:
\[\frac{∂}{∂ϕ_l} \sum_{i=1}^{m}{w^{(i)}_{l} log ϕ_l} = λ \frac{∂}{∂ϕ_l} \sum_{j}{ϕ_j} \\ \frac{1}{ϕ_l} \sum_{i=1}^{m}{w^{(i)}_{l}} = λ\]Use \(\sum_{j}{ϕ_j}=1\), we have
\[\sum_{j=1}^{m}{\frac{1}{λ}\sum_{i=1}^{m}{w^{(i)}_{j}}} = 1 \\ λ = m\]Note: Another way to do this is by substitute of variable, let \(ϕ_j = \frac{\exp \psi_j}{\sum \exp \psi_j }\)
So
\[ϕ_l = \frac{1}{m} \sum_{i=1}^{m}{w^{(i)}_{l}}\] -
\(\partial \mathbf{Σ}_l\).
\[J(Q,θ) = \sum_{i=1}^{m}{\sum_{j}{w^{(i)}_j log \frac{(2π)^{-\frac{n}{2}} |Σ_j|^{-\frac{1}{2}}exp{\left(-\frac{1}{2} (x^{(i)}-μ_j)^{T} Σ_j^{-1}(x^{(i)}-μ_j) \right)}ϕ_j}{w^{(i)}_j}}} \\ \begin{align} \frac{∂J}{∂({Σ_l}^{-1})} &= \frac{∂}{∂({Σ_l}^{-1})} \sum_{i=1}^{m}{w^{(i)}_{l} log \frac{(2π)^{-\frac{n}{2}} |Σ_l|^{-\frac{1}{2}}exp{\left(-\frac{1}{2} (x^{(i)}-μ_l)^{T} Σ_l^{-1}(x^{(i)}-μ_l) \right)ϕ_j}}{w^{(i)}_{l}}} \\ &= \frac{∂}{∂({Σ_l}^{-1})} \sum_{i=1}^{m}{w^{(i)}_{l} log \left({|Σ_l|^{-\frac{1}{2}}exp{\left(-\frac{1}{2} (x^{(i)}-μ_l)^{T} Σ_l^{-1}(x^{(i)}-μ_l) \right)}} \right)} \\ &= \frac{∂}{∂({Σ_l}^{-1})} \sum_{i=1}^{m}{w^{(i)}_{l} \frac{1}{2} log {|Σ_l|^{-1}}} + \frac{∂}{∂({Σ_l}^{-1})} \sum_{i=1}^{m}{w^{(i)}_{l}\left(-\frac{1}{2} (x^{(i)}-μ_l)^{T} Σ_l^{-1}(x^{(i)}-μ_l) \right)} \\ &= \frac{∂}{∂({Σ_l}^{-1})} \sum_{i=1}^{m}{w^{(i)}_{l} log {|Σ_l|^{-1}}} - \frac{∂}{∂({Σ_l}^{-1})} \sum_{i=1}^{m}{w^{(i)}_{l}\left((x^{(i)}-μ_l)^{T} Σ_l^{-1}(x^{(i)}-μ_l) \right)} \\ &= \sum_{i=1}^{m}{w^{(i)}_{l}{Σ_l}} - \sum_{i=1}^{m}{w^{(i)}_{l}\left((x^{(i)}-μ_l)(x^{(i)}-μ_l)^{T} \right)} \end{align}\]Set to 0, we have
\[Σ_l = \frac{\sum_{i=1}^{m}{w^{(i)}_{l}\left((x^{(i)}-μ_l)(x^{(i)}-μ_l)^{T} \right)}}{\sum_{i=1}^{m}w^{(i)}_{l}}\]
-
-
 This work is licensed under Creative Commons BY-NC-ND 3.0 Unported License.
This work is licensed under Creative Commons BY-NC-ND 3.0 Unported License.