Inequality Notes
Notes on Inequality
-
实数上的平均值不等式
若 \(a,b > 0,\, a,b \in \mathbb{R}\), 则
\[\sqrt{ab} \leq \frac{a+b}{2} \leq \sqrt{\frac{a^2+b^2}{2}}\]证:
\[\begin{aligned} \sqrt{ab} &= \sqrt{ \left( \frac{a+b}{2} + \frac{a-b}{2} \right) \left( \frac{a+b}{2} - \frac{a-b}{2} \right) } \\ &= \sqrt{ \left( \frac{a+b}{2} \right)^2 - \left( \frac{a-b}{2} \right) ^2 } \\ &\leq \sqrt{ \left( \frac{a+b}{2} \right)^2 } \\ &= \frac{a+b}{2} \\ &\leq \sqrt{ \left( \frac{a+b}{2} \right)^2 + \left( \frac{a-b}{2} \right) ^2 } \\ &= \sqrt { \frac{a^2 + b^2}{2} } \end{aligned}\]注意这里可以有一些弹性的变换,如:
\[ab \leq \frac{1}{2}\epsilon a^2 + \frac{1}{2}\frac{b^2}{\epsilon},\, \forall \epsilon > 0\] -
AM-GM不等式
虽然此时还没有长度,面积,体积等的定义,但是直觉理解是:\(\frac{a+b}{2}\) 是平均边长,\(\sqrt{ab}\) 是等体积的正方形的平均边长。
所以 \(\sqrt{ab} \leq \frac{a+b}{2}\) 的意思是说,在等面积长方形中,正方形是平均边长最小的。
当然这也可以扩展到多维之中,自然的,我们推测:
\[\sqrt[n]{x_1x_2\cdots x_n} \leq \frac{x_1 + x_2 + \cdots + x_n}{n},\, x_i > 0\]Proof by induction (From Wikipedia):
Suppose it holds for integers ≤ n.
Let \(\alpha = \frac{1}{n} \left( x_1 + \cdots + x_{n+1} \right)\), Suppose \(x_n > \alpha\) and \(x_{n+1} < \alpha\) (by reordering, If such reordering cannot be done, it means that all x_i are equal).
Let \(y\) be \(x_n + x_{n+1} - \alpha\), so that \(\alpha\) is also the mean of \(x_1, \cdots, x_{n-1}, y\). By induction we have.
\[\alpha^{n+1} = \alpha^n \alpha \geq x_1x_2\cdots x_{n-1}y\alpha\]All we need to do is to proof \(y\alpha > x_nx_{n+1}\)
\[\begin{aligned} y\alpha - x_nx_{n+1} &= (x_n+x_{n+1}-\alpha)\alpha - x_nx_{n+1} \\ &= (x_n-\alpha)(\alpha-x_{n+1}) > 0 \end{aligned}\]Hence \(\alpha^{n+1} > x_1x_2\cdots x_{n+1}\) If x_i are not all the same.
-
Weighted AM–GM inequality
if \(w_i\) are positive integers, we can easily have
\[\sqrt[w]{x_1^{w_1}x_2^{w_2}\cdots x_n^{w_n}} \leq \frac{w_1x_1 + w_2x_2 + \cdots + w_nx_n}{w},\, x_i > 0\]where \(w = \sum_{i}{w_i}\).
if \(w_i\) are positive rationals, by finding the lcm (想办法通分), it also holds.
if \(w_i\) are real numbers, by basic analysis, it still holds.
-
常用复数上的不等式
Let \(z = x + yi\), by definition
\[\left\vert z \right\vert ^2 = z \cdot \overline{z} = x^2 + y^2 = \operatorname{Re } (z)^2 + \operatorname{Im } (z)^2\]所以
\[\left\vert z \right\vert \geq \left\vert \operatorname{Re } (z) \right\vert ,\,\,\,\, \left\vert z \right\vert \geq \left\vert \operatorname{Im } (z) \right\vert\] \[\begin{aligned} \left\vert \left\vert z+w \right\vert ^2 \right\vert &= (z+w) \left\vert \left( z+w \right) \right\vert \\ &= (z+w) \left( \left\vert z \right\vert + \left\vert w \right\vert \right) \\ &= \left\vert z \right\vert^2 + \left\vert w \right\vert ^2 + (z \overline{w} + \overline{z} w) \\ &= \left\vert z \right\vert^2 + \left\vert w \right\vert ^2 + 2 \operatorname{Re } (z \overline{w}) \\ &\leq \left\vert z \right\vert^2 + \left\vert w \right\vert ^2 + 2 \left\vert z \overline{w} \right\vert \\ &= \left\vert z \right\vert^2 + \left\vert w \right\vert ^2 + 2 \left\vert z \right\vert \left\vert w \right\vert \\ &= \left( \left\vert z \right\vert + \left\vert w \right\vert \right) ^2 \end{aligned}\]所以
\[\left\vert z+w \right\vert \leq \left\vert z \right\vert + \left\vert w \right\vert\]最后,有
\[\left\vert \left\vert w \right\vert - \left\vert z \right\vert \right\vert \leq \left\vert w - z \right\vert\] -
柯西-施瓦茨不等式(Cauchy Schwarz inequality)
更新:内积是柯西-施瓦茨不等式的抽象,在另一篇笔记的6.15节看到了这个不等式,以下有部分是过时的原始内容:
这篇文章:向量分析-Cauchy-Schwarz不等式之本質與意義-林琦焜 (缓存)写的非常好。
在思考内积时,不能用欧式空间/余弦定理等,而要抽象成不依赖空间的东西,再用内积定义角度,神奇的是,角度定义可以不止一种,甚至可以是复数。
-
证法一:
如果 \(a_1, a_2, \cdots, a_n, \text{ and } b_1, b_2, \cdots, b_n\) 都是复数,那么
\[\left\vert \sum_{i=1}^{n}{a_i\overline{b}_i} \right\vert^2 \leq \left( \sum_{i=1}^{n}{\lvert a_i \rvert^2} \right) \left( \sum_{i=1}^{n}{\lvert b_i \rvert^2} \right)\]证:设\(a,b\)是复向量, \(a≠0\),\(λ\)是标量,\(c = b - λa\)
\[0 ≤ \lvert c \rvert = c \overline{c} = (b-λa) (\overline{b} - λ \overline{a})\]对\(λ\)应用判别式Δ≤0,得:
\[( b \overline{a} + a \overline{b} )^2 ≤ 4 \lvert a \rvert ^2 \lvert b \rvert ^2 \\ ( b \overline{a} )^2 + (a \overline{b} )^2 ≤ 2 \lvert a \rvert ^2 \lvert b \rvert ^2\]注意到 \(b \overline{a} = \overline{b \overline{a}}\),所以
\[( a \overline{b} )^2 ≤ \lvert a \rvert ^2 \lvert b \rvert ^2\] -
证法二:
由平均值不等式, \(\sqrt{ab} \leq \sqrt { \frac{1}{2}a^2 + \frac{1}{2}b^2 }\), 令
\[\widetilde{a}_i = \frac{a_i}{\sqrt{\sum_{i=1}^{n}{a_i^2}}},\,\,\,\, \widetilde{b}_i = \frac{b_i}{\sqrt{\sum_{i=1}^{n}{b_i^2}}}\]则
\[\widetilde{a}_i \widetilde{b}_i \leq \frac{1}{2}\widetilde{a}_i^2 + \frac{1}{2}\widetilde{b}_i^2\]两边对\(i\)求和
\[\sum_i { \widetilde{a}_i \widetilde{b}_i } \leq \sum_i { \frac{1}{2}\widetilde{a}_i^2 + \frac{1}{2}\widetilde{b}_i^2 }\]a.k.a.
\[\frac{\sum_{i}^{n}a_ib_i}{\sqrt{\sum_{i=1}^{n}{a_i^2}}\sqrt{\sum_{i=1}^{n}{b_i^2}}} \leq 1\]a.k.a
\[\sum_{i}^{n}a_ib_i \leq \sqrt{\sum_{i=1}^{n}{a_i^2}}\sqrt{\sum_{i=1}^{n}{b_i^2}}\]在实数成立之后,由 \(\left\vert z+w \right\vert \leq \left\vert z \right\vert + \left\vert w \right\vert\) 要叫推出在复数上也成立
\[\left\vert \sum_{i}^{n}a_ib_i \right\vert \leq \sum_{i}^{n}{\left\vert a_ib_i \right\vert} = \sum_{i}^{n}{ \left\vert a_i \right\vert \left\vert b_i \right\vert }\]
-
-
杨氏不等式(Young’s inequality)
\[ab ≤ \int_0^a{f(x)} + \int_0^b{f^{-1}(y)}\]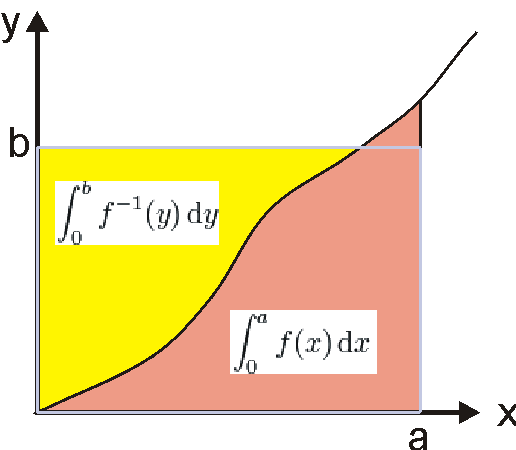
令 \(f(x) = x^{p-1} \text{ where p > 1 }\) 可得
\[ab ≤ \frac{a^p}{p} + \frac{b^q}{q} \text{ where } a,b>0,\,\frac{1}{p} + \frac{1}{q}=1\]等号成立条件为 \(b = a^{p-1}\) ,亦即 \(a = b^{q-1}\) 亦即 \(a^p = b^q\)
另一种比较代数的证明方式见 https://math.stackexchange.com/a/259837
-
Hölder不等式(实数版)
给定任意实数\(a_1, \cdots, a_n,\, b_1, \cdots, b_n,\, p>1,\, q>1,\, \frac{1}{p} + \frac{1}{q} = 1\)则:
\[\sum_{i=1}^{n}{a_ib_i} ≤ \left( \sum_{i=1}^{n} \left\vert a_i \right\vert ^p \right) ^ { \frac{1}{p} } \left( \sum_{i=1}^{n} \left\vert b_i \right\vert ^q \right) ^ { \frac{1}{q} }\]证:仿效柯西不等式证法二:令
\[\widetilde{a}_i = \frac{a_i}{\left( \sum_{i=1}^{n} \left\vert a_i \right\vert ^p \right) ^ { \frac{1}{p} }},\, \widetilde{b}_i = \frac{b_i}{\left( \sum_{i=1}^{n} \left\vert b_i \right\vert ^q \right) ^ { \frac{1}{q} }},\]则由杨式不等式,左右累加并化简得 \(\sum{\widetilde{a}_i \widetilde{b}_i} ≤ 1\),又分母大于0,所以分子小于分母,即为所求。
 This work is licensed under Creative Commons BY-NC-ND 3.0 Unported License.
This work is licensed under Creative Commons BY-NC-ND 3.0 Unported License.